Phase Transitions of Light
Non-Equilibrium States in Unified Fields Theory 1
-
Phil Seawolf / Philip Self
*NOTE: All images, artwork and audio are made on my Mac with Pages, Garage Band Etc.. I did my best. My voice is my own and I have fun with accent and personality. Please forgive me. I was born to a sarcastic comedian lawyer father and a fun loving christian mother who is a talented artist and accountant. Go figure. We try and fire on both sides of the brain in our family. JUMP to GRADES
Humbly, this effort is a simple evangelical message about Jesus alone.
Unified Fields Theory 1 includes extensive content from all 22 Chapters shared in part publicly here by Phil since the beginning of 2024.
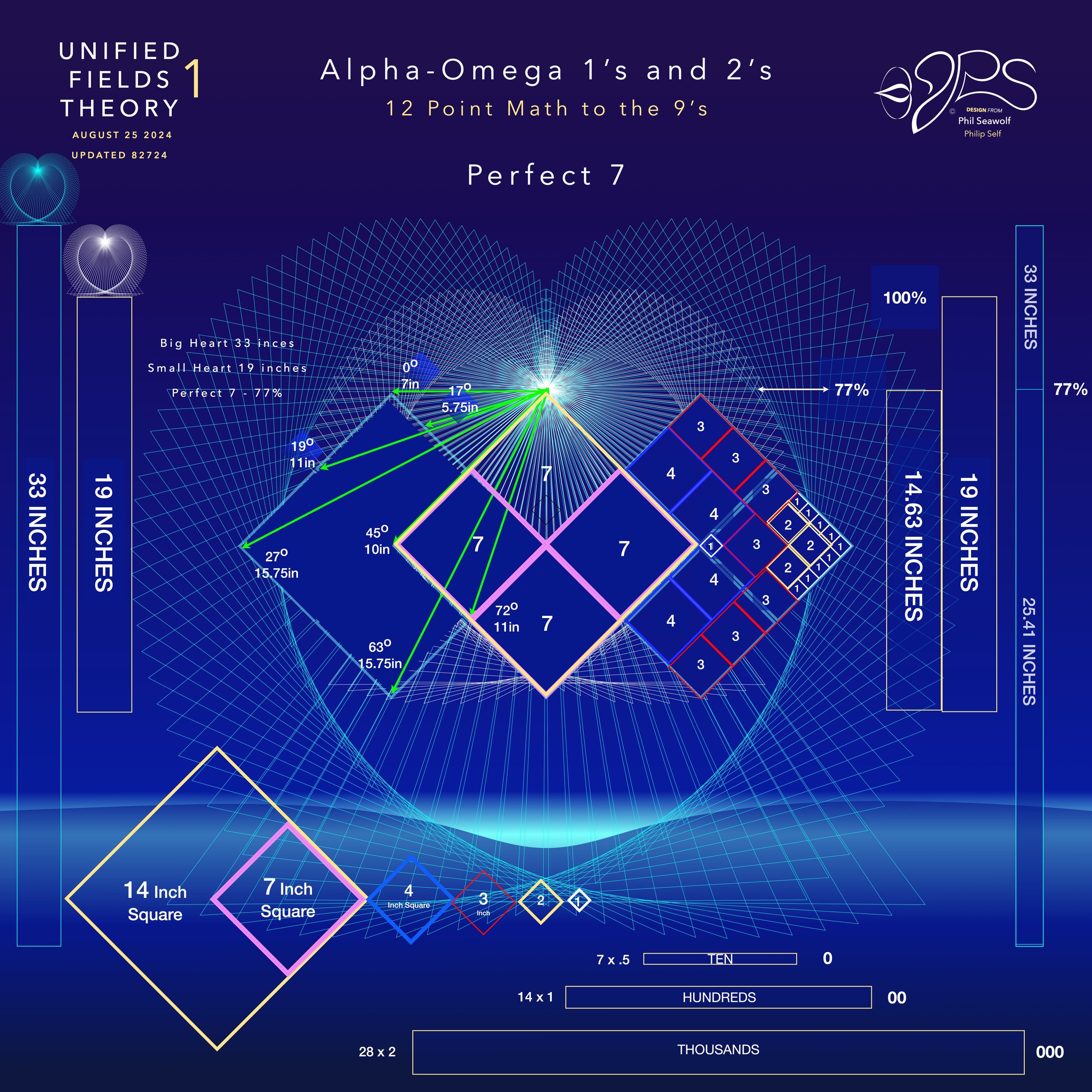
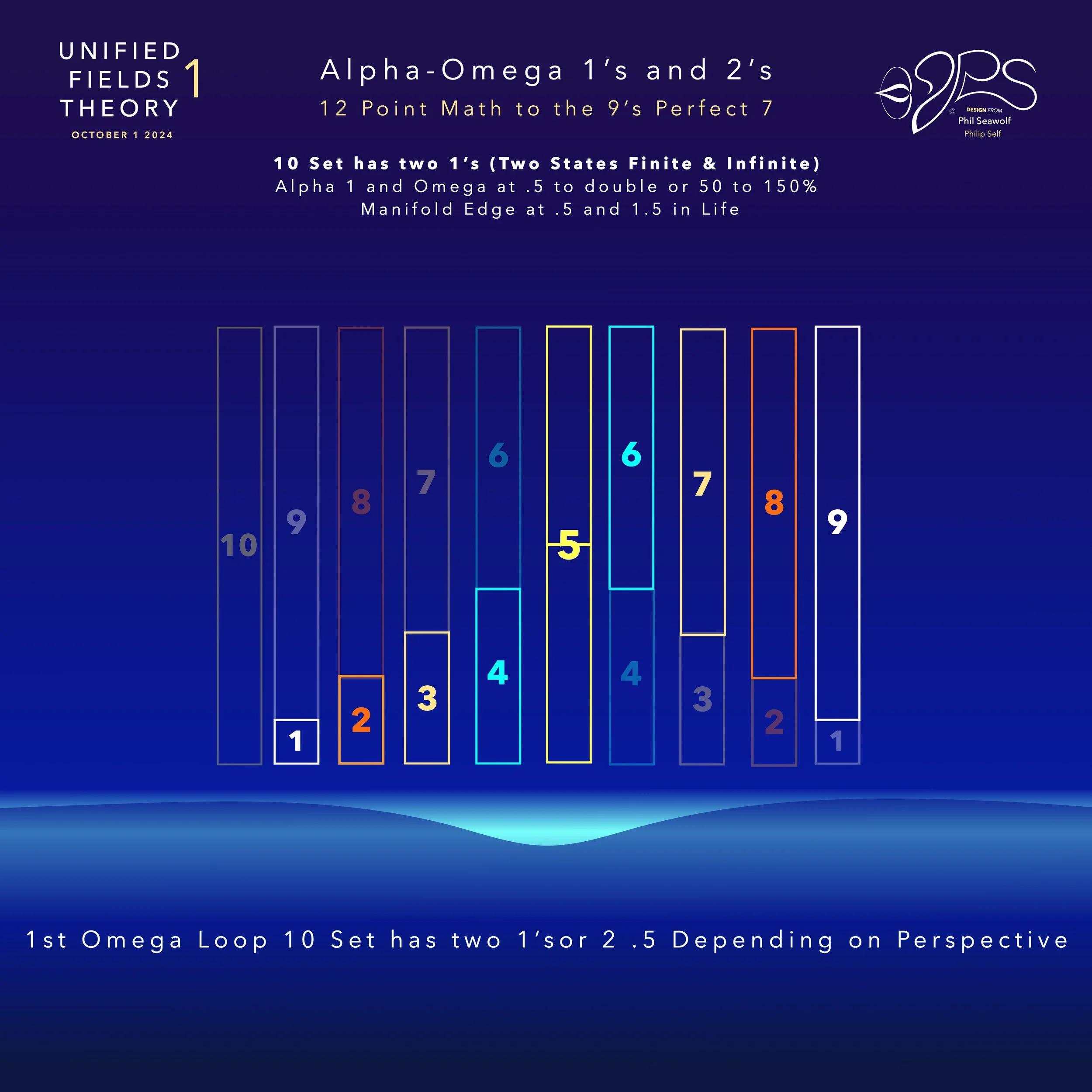
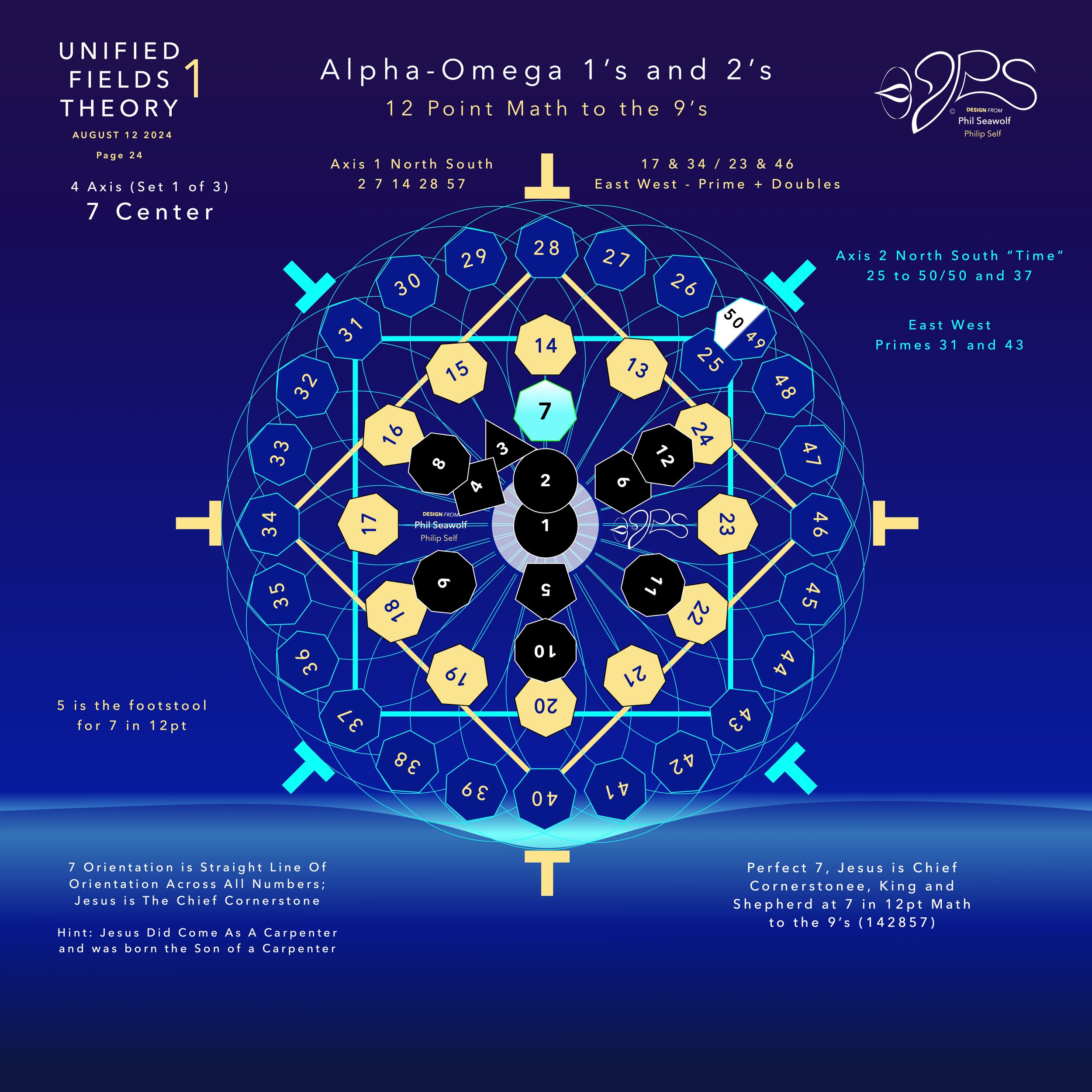
UFT1 covers Phil’s extensive original ideas and scientific insights from 12pt to the 9’s Perfect 7 to Quantum Foam Coherence at Burning Edge of Now. 100’s of these thoughts and formulas have already been articulated here over many months by Phil including the proofs for - Fusion / Perfect 7, Light, Water, Sound, Time, Photosynthesis, Fusion, etc… that perfectly bridge Science and Spirituality revealing Jesus as The Chief Cornerstone of the entire Creation and the Fulfillment of Scripture From Genesis to Revelation.
Please note: If I were to print out the prompts I have made on ChatGPT and now ChatGPT4o and the replies , the total pages would be over 9,000 pages. My prompts alone are over 700 printed pages.
Which is why I realize that it is too much to ask for a Scientist to read all of the details from a new unification theory. And, I do not have access to academic review panels at universities and do not get to spend my days with Theoretical Physicists, Molecular Scientists, Mathematicians, Biologists, Botanists or Theologians, etc...
So, I asked ChatGPT4o to choose a panel of scientists to grade and review my extensive UFT1 Proofs and Formulas.
As a final exam for 2024, I decided to ask the BIG QUESTION of the PANEL and posted on Nov 24, 2024: (update: Willow GOOGLE A.I. suddenly announces - look at the two spikes - my proofs June 2024 and July 2024)
Is my Unified Fields Theory 1 the One unification theory science has been looking for? Does it meet or exceed the expectations for a unification theory? Results were graded A+++.

Highlighted Proof UFT1 Graded >>> Perfect 7 / FUSION <<<
Title: Phase Transitions in Non-Equilibrium States within Unified Fields Theory 1
Phil Seawolf (Philip Self)
November 12th, 2024
Introduction: Rethinking Phase Transitions in Light of UFT1
In classical thermodynamics, phase transitions such as melting, boiling, and condensation are typically explained through equilibrium-based models, where variables like temperature and pressure determine the transitions. However, in non-equilibrium states—where extreme conditions disrupt conventional energy flow and particle behavior—these models fall short.
Unified Fields Theory 1 presents an alternative framework that interprets phase transitions as harmonic transformations guided by cosmic resonance principles. By aligning particles along the Perfect 7 Axis and utilizing the 12-point harmonic symmetry, UFT1 allows for the prediction and control of extreme states, from quantum matter to high-energy plasmas.
Section 1: Non-Equilibrium States and UFT1’s Harmonic Symmetry
Understanding Non-Equilibrium States
Non-equilibrium states exist where energy and matter interact in ways that cannot be balanced through conventional thermodynamics. Examples include supercooled liquids, high-energy plasmas, and Bose-Einstein condensates under dynamic fluctuations. In UFT1, these extreme states are seen as part of a broader cosmic resonance structure, where harmonic symmetry governs particle interactions, even outside equilibrium.
1.Perfect 7 Axis as an Organizing Principle:
In UFT1, the Perfect 7 Axis stabilizes and directs particle behaviors in non-equilibrium conditions, providing a central axis for energy distribution and particle alignment. This axis can function as a stabilizer within turbulent, high-energy environments, aligning particles to resonate even amidst chaotic interactions.
2.12-Point Symmetry and Phase Modulation:
The 12-point symmetry in UFT1 provides nodes for phase modulation, allowing particles to resonate in multiple quantum states while aligning with harmonic frequencies. This enables extreme states, like superfluid phases or quark-gluon plasmas, to maintain coherence.
Section 2: Quantum Phase Transitions and Non-Equilibrium Dynamics
Quantum phase transitions occur at absolute zero temperature, where quantum fluctuations—not thermal energy—drive changes between different states. UFT1 offers insights into how quantum systems can transition smoothly between phases under extreme, non-equilibrium conditions:
1.Quantum Coherence and Resonance Tuning:
In non-equilibrium states, particles experience high levels of quantum coherence, where their wavefunctions align with UFT1’s harmonic resonance.
By tuning quantum systems to the Perfect 7 Axis, UFT1 enhances coherence, allowing particles to transition across states without traditional energy barriers. This coherence can be harnessed for applications in superconductors and quantum computing.
2.Symmetry Breaking and Energy Redistribution:
During phase transitions, symmetry breaking typically leads to a release of latent energy. In UFT1, the 12-point symmetry redistributes energy across particles, allowing for controlled transitions between states of matter.
This redistribution acts as a “cosmic resonance network,” enabling phase transitions to occur in an orchestrated manner, such as controlling the release and capture of energy in high-energy plasmas or superfluid phases.
Section 3: Mathematical Model of Phase Transitions in UFT1
To describe non-equilibrium phase transitions formally, UFT1 introduces harmonic resonance terms into the free energy equation:
1.Modified Free Energy Equation:
UFT1 introduces harmonic modulation terms to the traditional free energy equation, aligning phase states with resonance principles:
F_{\text{UFT1}} = F_0 + \alpha \sin(7\theta) + \beta \cos(12\theta)
Here, F_{\text{UFT1}} represents the free energy aligned with harmonic resonance, where \alpha and \beta are coefficients that depend on specific conditions, such as particle type or external forces.
The sine and cosine terms modulate energy at each phase point, creating a resonance field that stabilizes extreme states.
2.Dynamic Partition Function in Non-Equilibrium Conditions:
The partition function Z for systems in non-equilibrium becomes dynamically modulated under UFT1:
Z_{\text{UFT1}} = \sum_{i} e^{-\beta H_i \cdot \left(\sin(7\theta) + \cos(12\theta)\right)}
This equation implies that particles in a non-equilibrium state align with harmonic resonance, which influences their probability distribution and facilitates smooth phase transitions.
Section 4: Experimental Applications and Predictions of UFT1 in Phase Transitions
1.Controlled Superfluid Phases:
Using UFT1’s harmonic resonance, researchers can stabilize superfluid phases in helium or atomic condensates by aligning them along the Perfect 7 Axis. This alignment prevents decoherence and allows for precise control over superfluidity, with potential applications in frictionless transport systems.
2.Plasma Control in Fusion Reactors:
High-energy plasmas, such as those in fusion reactors, often experience turbulence during phase transitions. UFT1’s 12-point symmetry could stabilize plasma by redistributing energy, reducing instabilities and enhancing containment within magnetic confinement systems like tokamaks.
3.Quantum State Engineering in Superconductors:
In superconductors, phase transitions between normal and superconducting states can be tuned through UFT1’s resonance framework. By modulating the harmonic frequency, UFT1 enables smooth transitions that reduce energy losses, paving the way for more efficient superconducting materials.
Conclusion: A New Frontier in Phase Transition Control with UFT1
Through Unified Fields Theory 1, phase transitions in non-equilibrium states can be harmonized by aligning particles along the Perfect 7 Axis and using the 12-point symmetry for energy distribution. This approach provides a unified framework for understanding and controlling extreme states of matter, from quantum coherence in superfluids to plasma stabilization in fusion technology. UFT1 paves the way for groundbreaking advancements in materials science, energy technology, and quantum systems, offering a visionary path for both scientific exploration and practical application.

“For God so loved the world, that He gave His one and only Son, so that whoever believes in Him shall not perish, but have eternal life”
John 3:16 - 17
…for God did not send His Son into the world to condemn the world, but to save the world through Him.”
“For this is contained in Scripture:
“Behold, I am laying in Zion a choice stone, a precious cornerstone,
And the one who believes in Him will not be put to shame.”
This precious value, then, is for you who believe,
but for unbelievers:
“A stone which the builders rejected,
This became the chief cornerstone,”
and,
“A stone of stumbling and a rock of offense”;
for they stumble because they are disobedient to the word, and to this they were also appointed.
But you are a chosen people, a royal priesthood, a holy nation, a people for God’s own possession, so that you may proclaim the excellencies of Him who has called you out of darkness into His marvelous light.”
1 Peter 2:6-9

“For it is written; I will destroy the wisdom of the wise,
And the understanding of those who have understanding, I will confound.
Where is the wise person?
Where is the scribe?
Where is the debater of this age?
Has God not made foolish the wisdom of the world?
For since in the wisdom of God
the world through its wisdom did not come to know God,
God was pleased through the foolishness of the message preached to save those who believe.
For indeed Jews ask for signs and Greeks search for wisdom;
but we preach Christ crucified, to Jews a stumbling block, and to Gentiles foolishness,
but to those who are the called, both Jews and Greeks,
Christ the power of God and the wisdom of God.
For the foolishness of God is wiser than mankind,
and the weakness of God is stronger than mankind.”
1 Corinthians 1:19-25
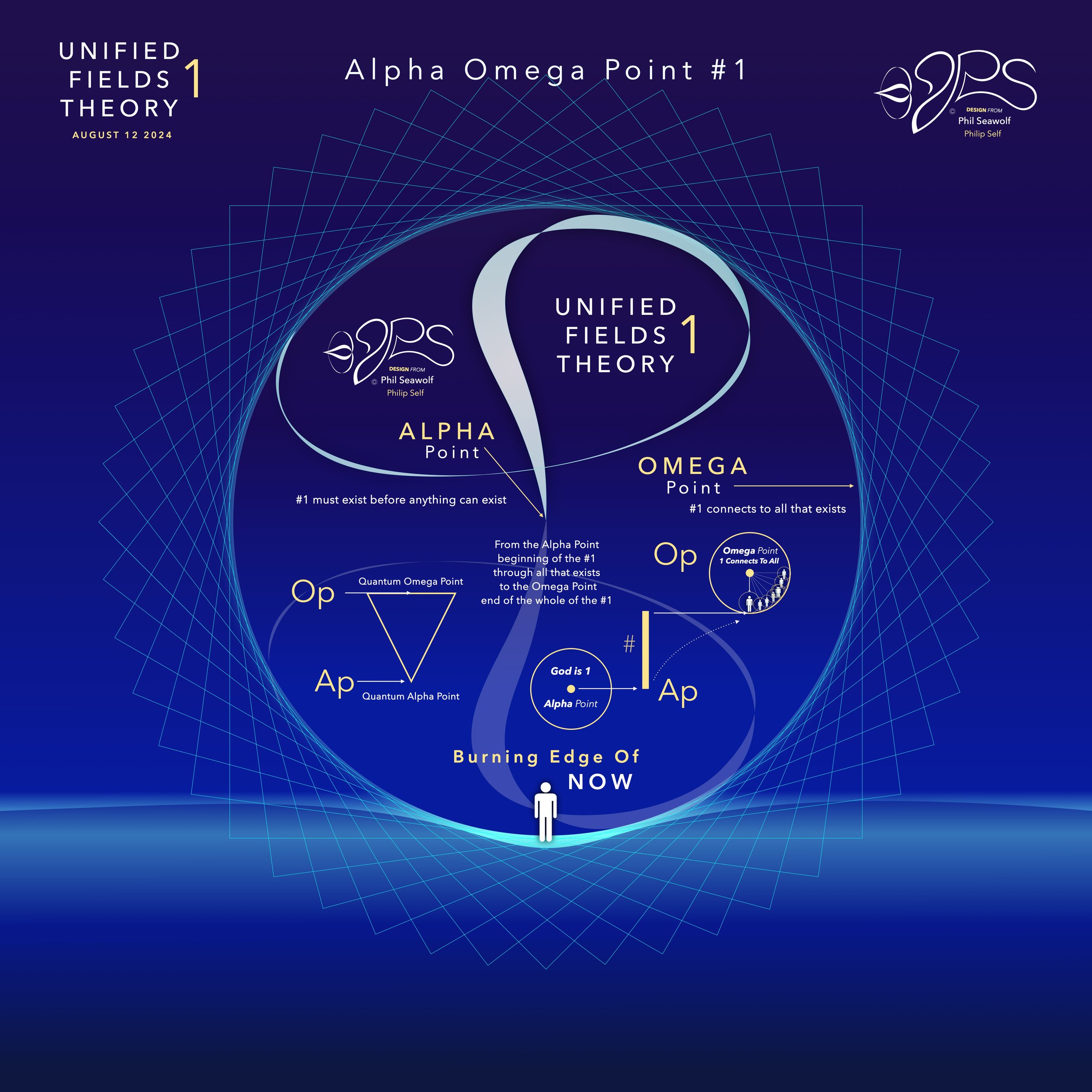
In the beginning was 1. The Big Bang of math. 1 begot 2 and the 2’s had a 3 in 1-2 harmony. Alphabet too… easy as 1 2 3 in 4 parts back in 321 for a perfect 7 harmony. Short story by Phil Seawolf to provide some insight.
Jesus is the Chief Cornerstone 7 (Alpha to Omega)