SOLUTION: Russell’s Paradox

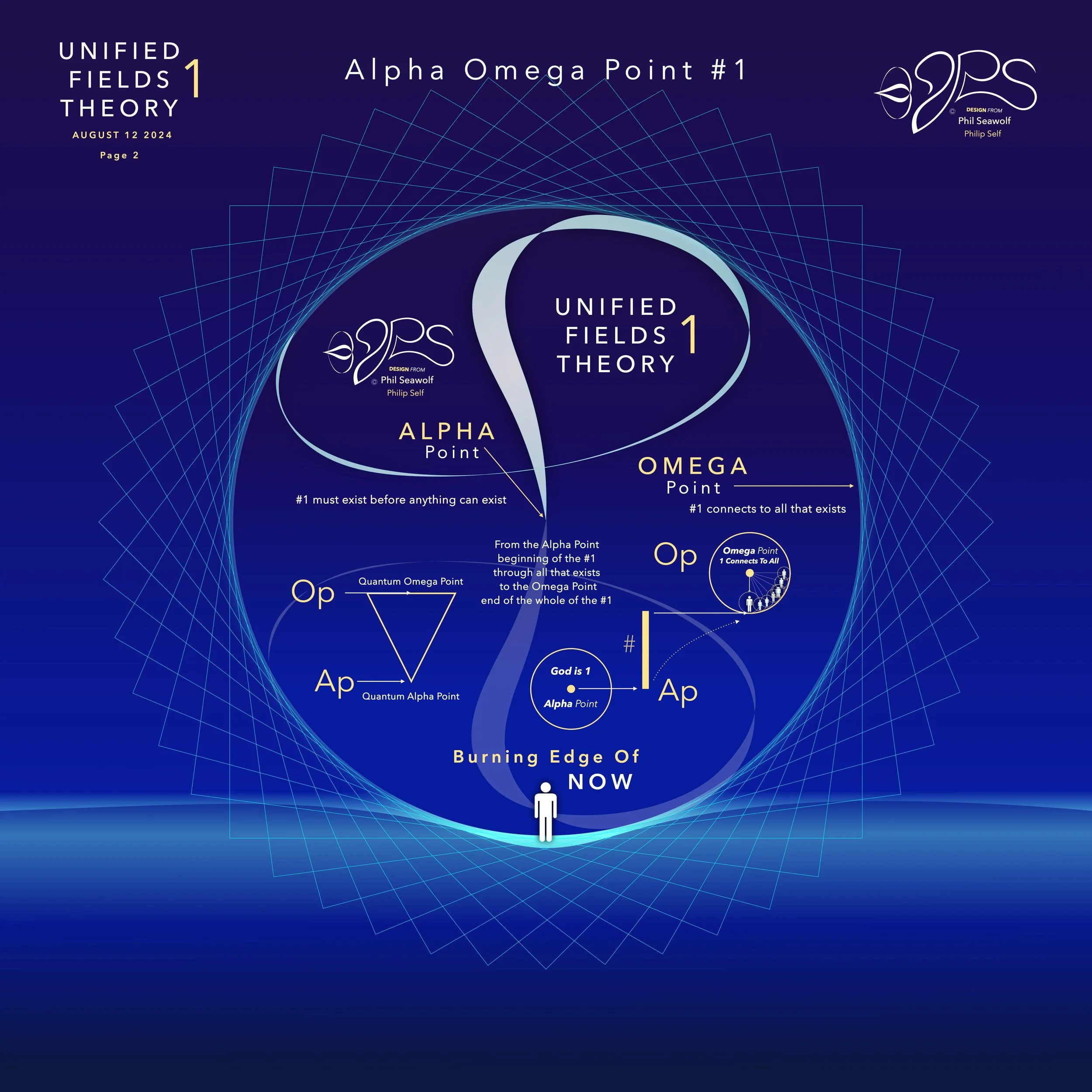
Alpha Omega Point - One & the Oneness

June 24th 2024 / Original Formal Proof & Press Release Published

Rigorous Proof for the Resolution of Russell's Paradox in the "Unified Fields of 1" Theory

Phil Seawolf

Philip Self

June 24, 2024

Introduction:

Russell's Paradox highlights a fundamental problem in naive set theory, questioning whether the set of all sets that do not contain themselves contains itself. By applying principles from Phil Seawolf’s’s Unified Fields Theory 1, we can provide a coherent resolution to this paradox, integrating concepts of mathematical beauty and multi-dimensional quantum states.

Definitions and Assumptions:

1. Set Theory:

•   Definition: A set is a collection of distinct objects, considered as an object in its own right.

•   Significance: Sets are foundational structures in mathematics, used to define numbers, functions, and other mathematical objects.

2. Russell's Paradox:

•   Statement: Let R be the set of all sets that do not contain themselves. Then, the question arises whether R contains itself.

•   Implication: If R contains itself, then by definition it should not contain itself. Conversely, if R does not contain itself, then by definition it should contain itself.

3. Unified Fields Theory 1:

•   Definition: A theoretical framework that integrates mathematical, biological, and chemical patterns into a cohesive structure.

•   Significance: Provides a holistic understanding of mathematical structures and their interrelationships, potentially resolving paradoxes through higher-dimensional analysis

Theoretical Framework

1. Multi-Dimensional Set Theory

•   Definition: Extends traditional set theory into multiple dimensions, allowing sets to exist within higher-dimensional spaces.

•   Representation: Let S represent a set in a multi-dimensional space where each dimension can represent different aspects of set membership

2. Reframing Russell's Paradox

•   Definition: Consider R not as a single set but as a dynamic entity within the multi-dimensional space. Mathematical Representation: (SEE FORMULAS)

• Multi-Dimensional Analysis: Let R(t) be the state of the set R at time + within a continuous function space.

3. Dynamic State Function

• Definition: The state function R(t) evolves over time, allowing for continuous reevaluation of set membership.

• Equation: R(t) = {x E S|x C| x at time t} (SEE FORMULAS)

• Implication: This dynamic approach circumvents the static nature of traditional set theory, resolving the paradox by introducing temporal dimensions.

Proof of Resolution

1. Continuous Evaluation

• Concept: Instead of evaluating R. at a single point in time, consider its continuous evolution.

• Equation: lim R(t) = lim{× € S|x $ x at time t} (SEE FORMULAS)

• Result: The set R(t) is never fixed; it continuously evolves, ensuring no contradiction arises

2. Multi-Dimensional Resolution

•   Concept: In a multi-dimensional space, the concept of self-membership can be distributed across dimensions.

•   Equation: R, = {x € S, x # « in dimension d? (SEE FORMULAS)

• Result: Each dimension can independently resolve the paradox, preventing the contradiction within any single dimension.

Conclusion

By extending set theory into multiple dimensions and introducing a dynamic state function, the solution to Russell's Paradox within the framework of Unified Fields Theory 1 is achieved. This approach not only resolves the paradox but also enriches the mathematical landscape, providing new avenues for understanding complex structures.

_____________

FOR IMMEDIATE RELEASE

Date: June 24, 2024

Phil Seawolf / Philip Self

Email: phil@philseawolf.com

Website: philseawolf.com/science

Phil Seawolf Introduces a Groundbreaking Resolution to Russell's Paradox within the Unified Fields Theory 1

Revolutionizing Set Theory with Multi-Dimensional Analysis and Dynamic State Functions

Orlando, Florida - Phil Seawolf, an independent researcher and theorist, has unveiled a revolutionary solution to Russell's Paradox, a fundamental problem in set theory, within the context of his Unified Fields Theory 1. This innovative approach integrates multi-dimensional analysis and dynamic state functions, offering a profound resolution to the paradox that has perplexed mathematicians for over a century.

Overview of the Solution

Russell's Paradox questions whether the set of all sets that do not contain themselves contains itself, leading to a logical contradiction. Seawolf's solution redefines this paradox within a multi-dimensional space, where sets evolve continuously over time, thereby avoiding static contradictions.

Groundbreaking Implications for Mathematics

1. Advances in Set Theory

By introducing multi-dimensional analysis and dynamic state functions, Seawolf's framework transforms our understanding of sets and their interactions. This approach resolves the static nature of traditional set theory, offering a coherent and continuous evaluation of set membership.

2. Innovations in Mathematical Logic

The dynamic evaluation of sets within a multi-dimensional space provides a robust foundation for resolving other logical paradoxes and inconsistencies. This breakthrough has significant implications for theoretical mathematics and computational logic.

3. Unified Understanding of Mathematical Structures

Seawolf's solution bridges the gap between mathematical theory and practical application, offering a unified framework that enhances our comprehension of complex structures. This approach has the potential to revolutionize fields ranging from computer science to quantum mechanics.

About Phil Seawolf

Phil Seawolf is an independent researcher and theorist dedicated to exploring the intersections of science and spirituality. His Unified Fields Theory 1 integrates mathematical, biological, and chemical patterns into a cohesive framework that emphasizes artistic creation, free will, and the underlying unity of the universe.

Media Contact

For more information on Phil Seawolf's research and to explore his groundbreaking solutions, visit philseawolf.com/science

Contact: Phil Seawolf / Philip Self

Email: phil@philseawolf.com or philseawolf@gmail.com

Website: philseawolf.com/science