SOLUTION: Hilbert’s Grand Hotel Paradox

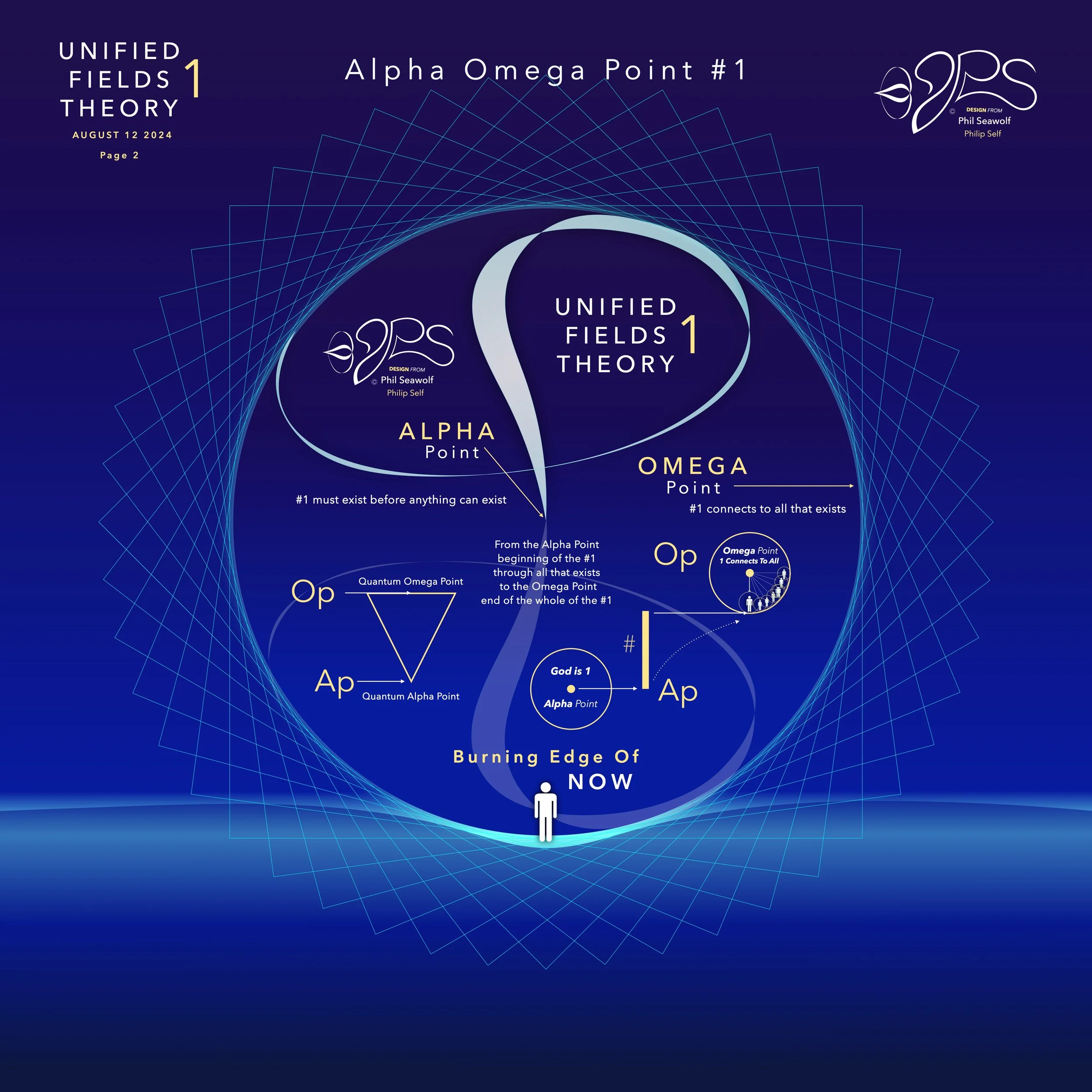
The Alpha Omega Line 1 & Unified Fields Theory

Updated Press Release July 17th 2024 / Formal Proof & Press Release Published (images below)

Phil Seawolf / Philip Self : July 17 2024

Formal Proof for the Solution to Hilbert’s Paradox of the Grand Hotel using the Alpha Omega Line of 1

**Scroll to bottom for images**

Introduction

Hilbert’s paradox of the Grand Hotel is a well-known thought experiment that highlights the counterintuitive nature of infinity. In this paradox, a hotel with an infinite number of rooms can always accommodate more guests, even if it is fully occupied. This proof from Phil Seawolf (Philip Self) utilizes the Alpha Omega Line of #1 from the Unified Fields Theory 1 to provide an elegant solution, emphasizing the "on" state, continuity, and dynamic symmetry in mathematical and physical realms.

Definitions and Assumptions

1.  Alpha Omega Line of #1:

•   Represents the continuum from the initial state (Alpha Point) to the final state (Omega Point), encompassing all intermediate states.

•   The state “on” at the Alpha Point persists through all subsequent points, including the Omega Point.

2.  Hilbert’s Paradox:

•    Involves a hotel with an infinite number of rooms, each occupied by a guest.

•    The paradox challenges the hotel to accommodate a new guest without displacing any current guests.

Theoretical Framework

1. Continuity of State “On”:

•   Let \( \alpha \) represent the Alpha Point where the state is “on”.

•   Let \( \omega \) represent the Omega Point, the culmination of infinite operations.

•   The Alpha Omega Line of #1 asserts that \( \alpha \) and \( \omega \) are connected by a continuous line, implying \( \omega = \alpha \) in terms of the state “on”.

2. Mathematical Representation:

•   Define the state function \( S(t) \) where \( t \) is time: \[ S(t) = \alpha \quad \forall \; t \in [0, \infty] \] (click to see formula)

•   For any subinterval \( [t_i, t_j] \subseteq [0, \infty] \): \[ S(t) = \alpha \]

Resolution of Hilbert’s Paradox

1. Initial State: “On”:

•  The initial state of “on” signifies that there is always an open state (vacancy) in the continuum.

• In the context of the hotel, this means that there is an inherent capacity to accommodate new guests without disrupting the existing configuration.

2. Dynamic Continuity:

• The Alpha Omega Line of #1 ensures dynamic continuity, meaning that the state of being “on” persists through all transitions and transformations.

• This dynamic nature allows for an infinite number of transitions (new guests) to be accommodated seamlessly.

3. Elegant Shift in Room Assignment:

•  When a new guest arrives, each guest can be thought of as existing in a dynamic state that allows for an infinite loop of occupancy:

•  \[ \text{Guest in room } n \rightarrow \text{Guest in room } n + 1 \] (click to see formula)

•  This shift is not just a linear progression but a manifestation of the continuous “on” state, ensuring no interruption in occupancy.

4. Implications for Infinity:

•   The “on” state at the Alpha Point implies an infinite capacity to accommodate new states (guests).

•   The Omega Point ensures that this infinite capacity remains intact, with the “on” state extending through all possible configurations of rooms.

Formula Representation

1. Room Shift Formula:

•   If \( n \) represents the room number and \( g(n) \) represents the guest in room \( n \), the new room assignment for accommodating an additional guest is: \ g(n) \rightarrow g(n+1) \] (click to see formula)

•   This results in room 1 being available for the new guest.

2. State Continuity Formula:

    - The state of room \( n \) being “on” (occupied) can be expressed as: \[ S_n = \alpha \quad \forall \; n \in \mathbb{N} \] (click to see formula)

    - The shift in room assignment maintains: \[ S_{n+1} = \alpha \] (click to see formula)

Conclusion

Phil Seawolf’s (Philip Self) Alpha Omega Line of #1 and the Unified Fields Theory 1 provide an elegant solution to Hilbert’s paradox of the Grand Hotel. By understanding the “on” state as a dynamic, continuous entity, we can accommodate an infinite number of transitions without disruption. This approach not only solves the paradox but also highlights the inherent beauty and symmetry of the universe, governed by the foundational principles of existence and motion. The grand narrative of mathematics and the cosmos is woven together in a seamless, infinite continuum, reflecting the profound wisdom and artistry of the divine design.

————————

Press Release

For Immediate Release

Date: July 17, 2024

Contact: Phil Seawolf

Email: phil@philseawolf.com

Groundbreaking Solution to Hilbert’s Paradox Revealed through Unified Fields Theory 1

*July 17, 2024* — In a remarkable breakthrough, Phil Seawolf’s Unified Fields Theory 1 has provided an elegant solution to Hilbert’s paradox of the Grand Hotel, a classic thought experiment that challenges our understanding of infinity.

The paradox, first introduced by German mathematician David Hilbert, imagines a hotel with an infinite number of rooms that are all occupied. When a new guest arrives, the paradox demonstrates that the hotel can still accommodate the guest by shifting each current guest to the next room. While traditionally used to illustrate the counterintuitive nature of infinity, Seawolf’s solution transcends mere illustration to provide a concrete mathematical framework.

Seawolf’s Unified Fields Theory 1 introduces the concept of the Alpha Omega Line of #1, which encapsulates the infinite set within a single, unbroken continuum. This model leverages the "on" state of existence, ensuring dynamic continuity and infinite capacity.

“The state of ‘on’ signifies a continuous state of existence, which inherently includes the capacity for an infinite number of transitions,” explains Seawolf. “In the context of Hilbert’s paradox, this means that our hotel can always accommodate more guests without disrupting the existing arrangement.”

This groundbreaking approach not only resolves the paradox but also underscores the inherent beauty and symmetry of the universe, which is woven together in a seamless, infinite continuum. The proof leverages dynamic room assignment and the continuity of state “on” to provide an elegant and practical solution.

Seawolf’s innovative thinking bridges the gap between mathematical theory and physical reality, offering profound implications for understanding the nature of infinity and continuity. The Alpha Omega Line of #1 is a cornerstone of the Unified Fields Theory 1, which seeks to unify various fields of science through a comprehensive and harmonious framework.

This revelation is set to have significant impacts on fields ranging from mathematics to theoretical physics, offering new insights and applications across disciplines.

For more information on Phil Seawolf’s Unified Fields Theory 1 and his work on solving mathematical paradoxes, please visit [www.philseawolf.com] or email phil@philseawolf.com philseawolf@gmail.com

About Phil Seawolf

Phil Seawolf is a visionary theorist whose work bridges the realms of mathematics, physics, and spirituality. His Unified Fields Theory 1 aims to unify diverse scientific disciplines through a coherent and elegant framework, highlighting the interconnectedness of the universe.