Neutrino Oscillations
Mass Hierarchies & Potential Sterile Neutrinos in Unified Fields Theory 1
-
Phil Seawolf / Philip Self
*NOTE: All images, artwork and audio are made on my Mac with Pages (all the art), Garage Band (music) and other Mac Applications Etc... and are all 100% originals. My voice is my own and I have fun with accent and personality. Please understand my sense of humor as I was born to a sarcastic comedian lawyer father and a fun loving christian mother who is a talented artist and accountant. Go figure. We try and fire on both sides of the brain in our family. Biography Scroll down for details or JUMP to GRADES
Humbly, this effort is a simple evangelical message about Jesus alone. Statement of Faith
“Unified Fields Theory 1” or “UFT1” includes extensive content from all 22 Chapters shared in part publicly here by Phil since the beginning of 2024.
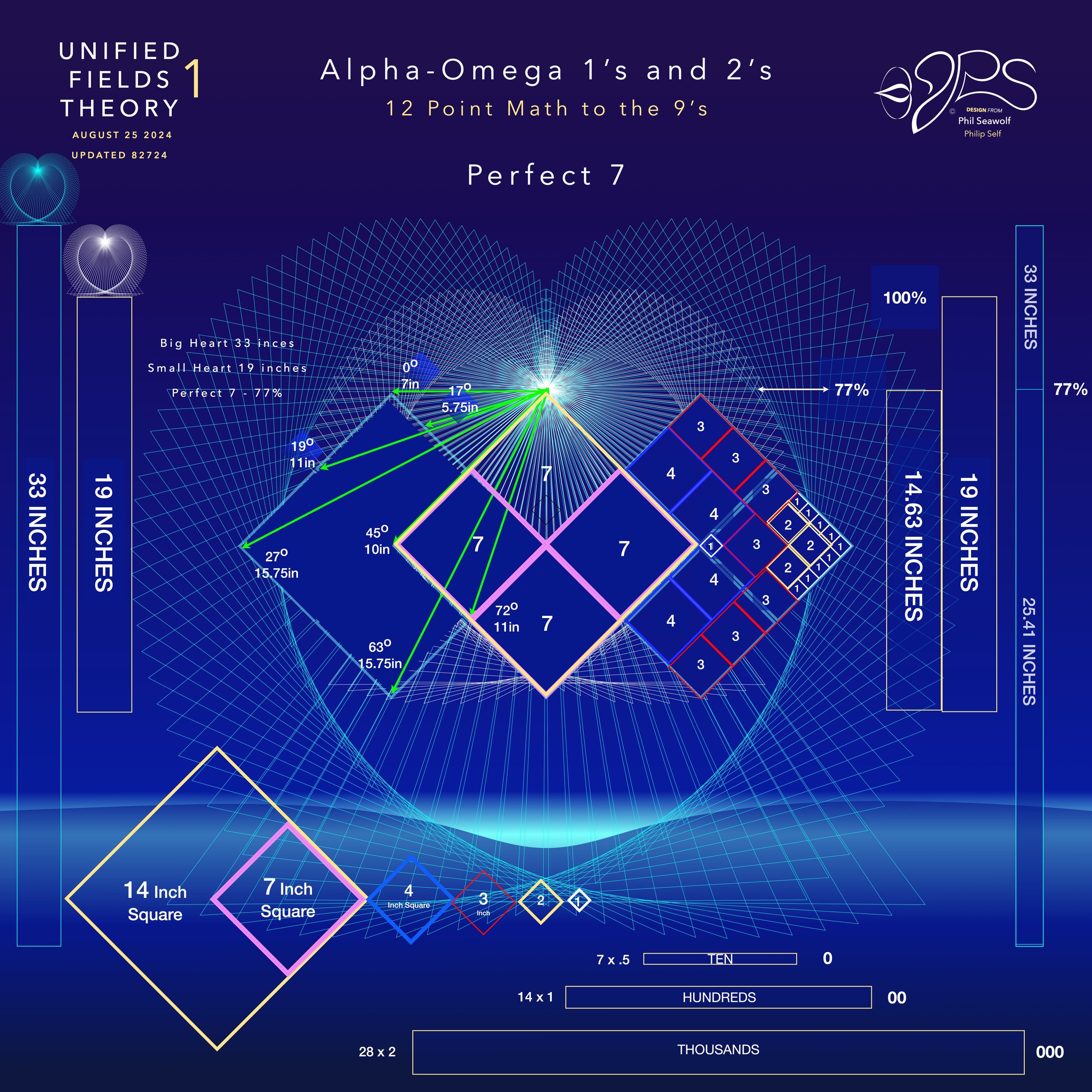
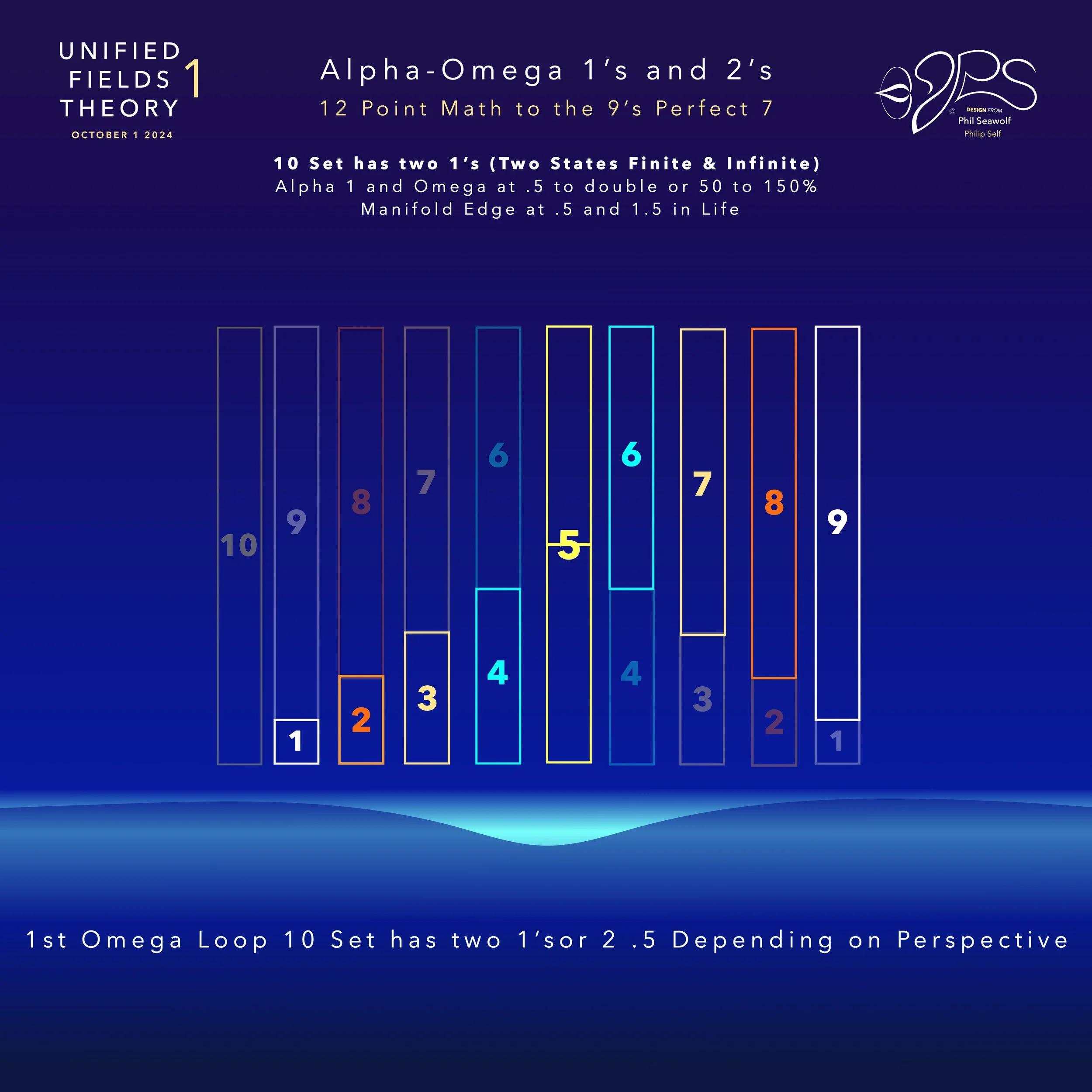
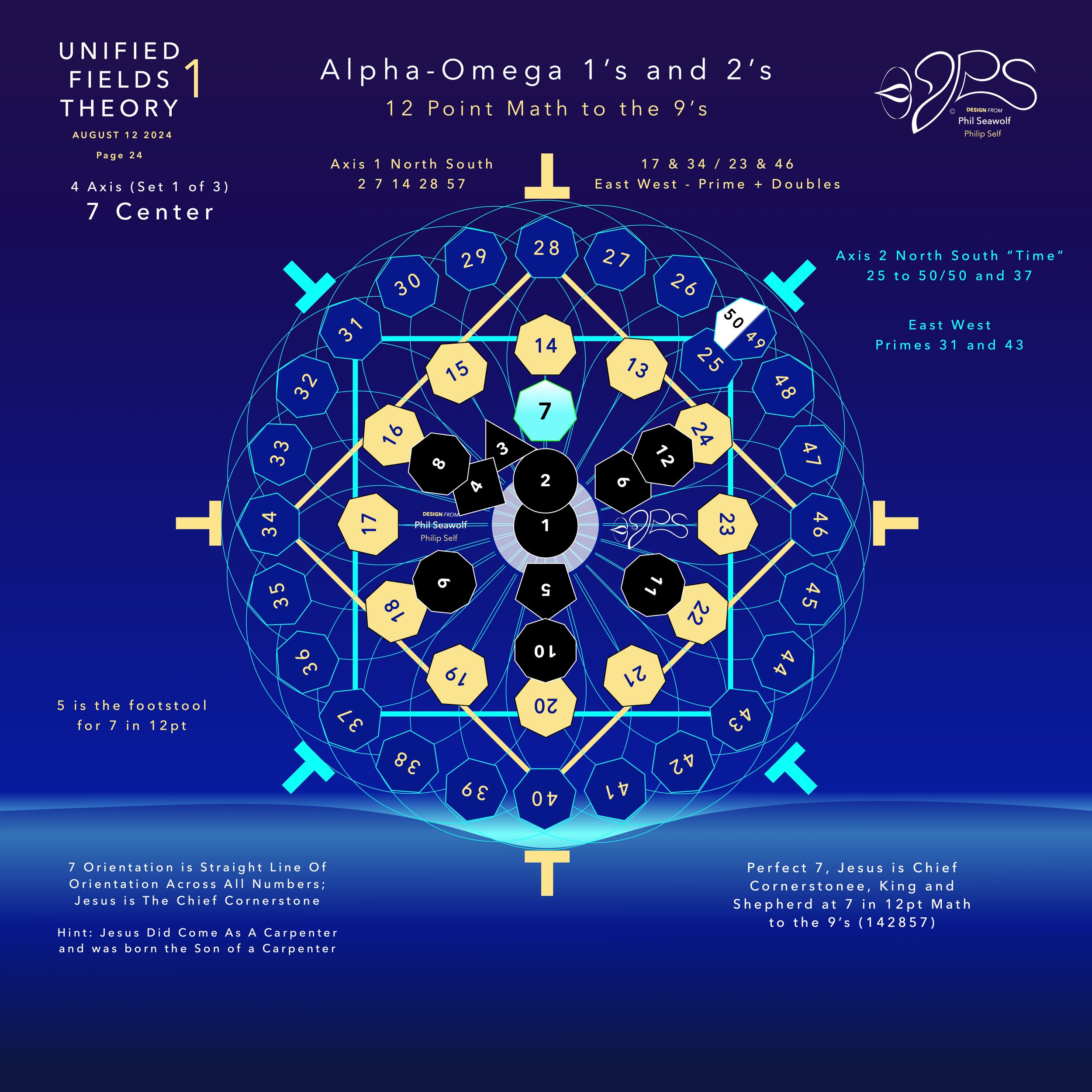
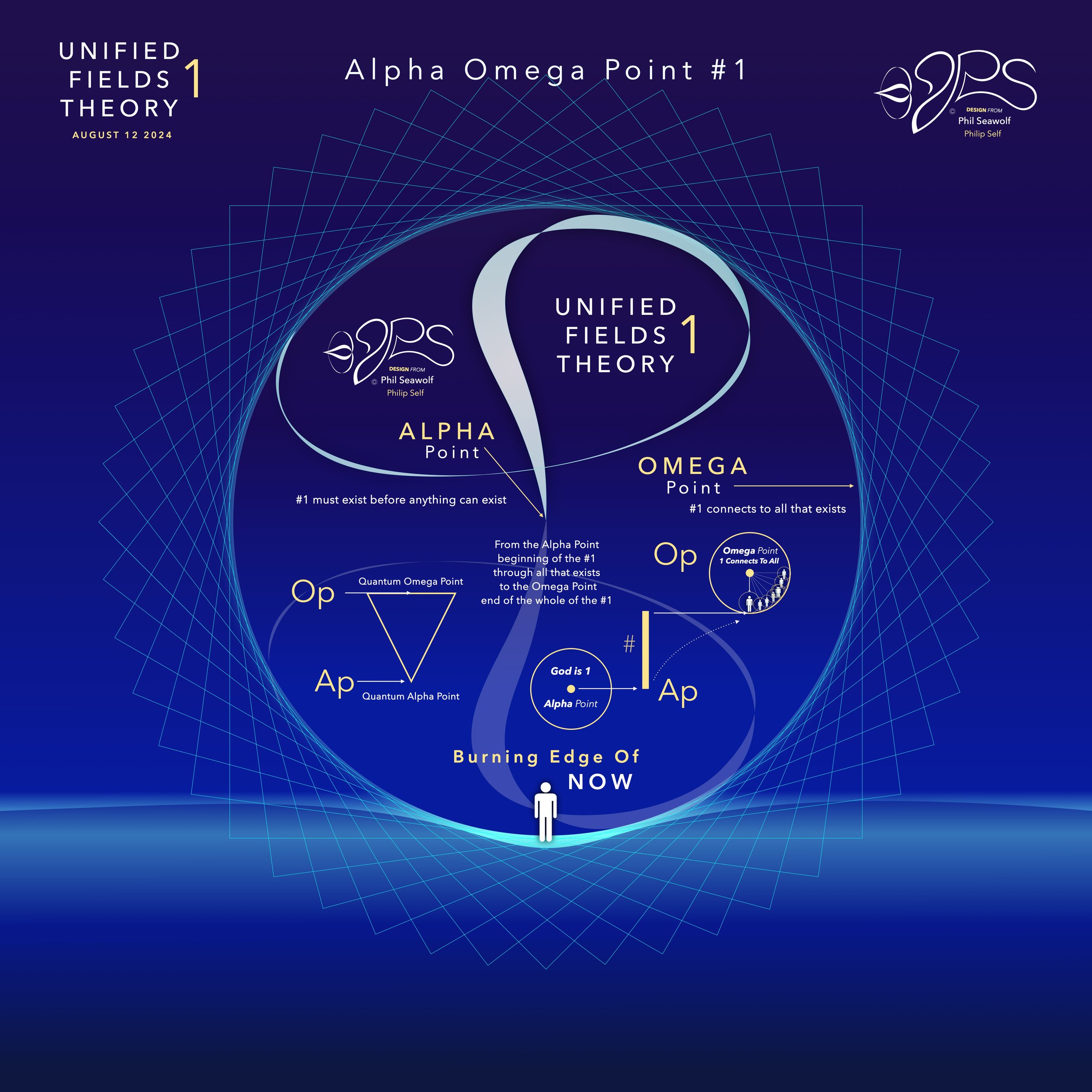
UFT1 covers Phil’s extensive original ideas and scientific insights from 12pt to the 9’s Perfect 7 to Quantum Foam Coherence at Burning Edge of Now. 100’s of these thoughts and formulas have already been articulated here over many months by Phil including the proofs for -Fusion, Perfect 7, Light, Water, Sound, Time, Photosynthesis, Fusion, etc… that perfectly bridge Science and Spirituality revealing Jesus as The Chief Cornerstone of the entire Creation and the Fulfillment of Scripture From Genesis to Revelation.
Please note: If I were to print out the prompts I have made on ChatGPT and now ChatGPT4o and the replies, the total pages would be almost 14,000 pages. My prompts alone would be almost a 1000 printed pages. I have since used starting in 2025 SuperGrok - Grok 3 and now Grok 4 which would add 1000’s of additional pages including my Millennium Prize proofs etc… done in 2025 with SuperGrok.. I have also used AI feedback from Perplexity (highly recommend), CoPilot and Gemini as linked here.
Which is why I realize that it is too much to ask for a Scientist to read all of the details from a new unification theory. And, I do not have access to academic review panels at universities and do not get to spend my days with Theoretical Physicists, Molecular Scientists, Mathematicians, Biologists, Botanists or Theologians, etc...
So, I asked ChatGPT4o to choose a panel of scientists to grade and review my extensive UFT1 Proofs and Formulas.
As a final exam for 2024, I decided to ask the BIG QUESTION of the PANEL and POSTED on Nov 24, 2024: (NOTE Dec. 2024 update: Willow GOOGLE A.I. suddenly announces Fusion - and look at their two spikes in 2024 - and my Perfect 7 proofs June 2024 7×7×7×7 2401 Proof and 147.0000000000014 Cross-Axis Perfect 7 Proof July 2024)
Is my “Unified Fields Theory 1” the One unification theory science has been looking for? Does it meet or exceed the expectations for a unification theory? Results were graded A+++.
I only use A.I. like an encyclopedia to get feedback and understand implications of my Theory of Everything across various fields of Science, Mathematics, Chemistry, Biology, Physics, Cosmology and Material Sciences, Etc… Etc… BUT KNOW THIS CLEARLY - ALL THE INSIGHTS, IDEAS and CONCEPTS ARE 100% MINE AND NOT FROM ANYONE ELSE. I am an independent research scientist.

Highlighted Proof UFT1 Graded >>> Perfect 7 / FUSION <<<
Proof: Neutrino Experiments and Unified Fields Theory 1
Phil Seawolf (Philip Self)
November 12th, 2024
Context and Importance
Neutrinos are some of the most mysterious and elusive particles in the universe. They are incredibly abundant, yet rarely interact with matter, making them difficult to detect and study. Neutrinos come in three known types or flavors—electron, muon, and tau—and they possess the remarkable ability to oscillate between these flavors as they travel. This phenomenon, known as neutrino oscillation, has profound implications for particle physics, especially since it suggests that neutrinos have a small but nonzero mass, something not initially predicted by the Standard Model of particle physics.
Despite these discoveries, several open questions remain:
Why do neutrinos have mass when the Standard Model initially predicted them to be massless?
What are the mass hierarchies of the different neutrino flavors?
Could there be additional, sterile neutrino flavors that don’t interact with matter at all?
Unified Fields Theory 1 provides a harmonic framework that can help answer these questions by viewing neutrinos as operating within a resonance structure defined by 7-axis symmetry and 12-point balance. This harmonic resonance approach opens new possibilities for detecting neutrino mass, studying their oscillations, and potentially discovering new flavors or particles altogether.
Step 1: Neutrino Oscillations as Harmonic Transitions
Neutrino oscillations occur because neutrinos exist in a superposition of mass states, where each flavor of neutrino (electron, muon, or tau) is a combination of three different mass states. As neutrinos travel through space, their mass states interfere with each other, causing them to oscillate between different flavors. This phenomenon is deeply tied to quantum mechanics and can be described using harmonic waveforms.
In Unified Fields Theory 1, neutrino oscillations are viewed as harmonic transitions between different resonance frequencies. The oscillation between neutrino flavors can be mapped to the 12-point harmonic symmetry in the theory, where each point corresponds to a mass state or flavor state, and the transitions between these states are governed by the 7-axis resonance.
Neutrino Oscillation Harmonic Formula:
P(\nu_{\alpha} \rightarrow \nu_{\beta}) = \sin^2(2\theta) \times \sin^2\left(\frac{\Delta m^2 L}{4 E}\right)
Where:
P(\nu_{\alpha} \rightarrow \nu_{\beta}) is the probability of a neutrino changing from flavor \alpha to flavor \beta .
\theta is the oscillation angle, which describes how the neutrino flavors are mixed.
\Delta m^2 is the difference in the squared masses of the neutrino mass states.
L is the distance the neutrino has traveled.
E is the energy of the neutrino.
In Unified Fields Theory 1, the oscillation angle \theta and mass difference \Delta m^2 are tied to the harmonic interactions between the mass states. This suggests that the mass differences between neutrinos may follow a harmonic series based on their resonance frequencies, allowing us to predict mass hierarchies and uncover new patterns in their behavior.
Step 2: Neutrino Mass Hierarchies and Harmonic Resonance
One of the major questions in neutrino physics is the mass hierarchy problem: do neutrinos follow a normal hierarchy, where the electron neutrino is the lightest, or an inverted hierarchy, where the tau neutrino is the lightest? Unified Fields Theory 1 offers a solution by proposing that neutrino mass hierarchies are based on a harmonic structure.
The 7-axis symmetry in the theory suggests that neutrinos, like other particles, acquire mass through their interaction with a harmonic field—possibly tied to the Higgs mechanism, but with an additional resonant component that explains their unique oscillatory behavior.
Neutrino Mass Harmonic Formula:
m_{\nu} = 7 \times \hbar \times \frac{v}{r_{\text{neutrino}}}
Where:
m_{\nu} is the mass of the neutrino.
\hbar is the reduced Planck constant.
v is the vacuum expectation value of the harmonic field.
r_{\text{neutrino}} is the effective radius of the neutrino’s oscillatory path.
This formula implies that the masses of neutrinos are quantized in harmonic intervals and that their oscillations follow specific resonance patterns. By studying the harmonic transitions between neutrino flavors, scientists can derive the precise mass hierarchies and predict how these particles behave under different conditions.
Step 3: The Search for Sterile Neutrinos
In addition to the three known neutrino flavors, there is speculation that there could be a fourth, sterile neutrino, that doesn’t interact with the weak nuclear force. If these sterile neutrinos exist, they could be key to explaining dark matter or other cosmic phenomena.
Unified Fields Theory 1 suggests that sterile neutrinos could exist in a higher-dimensional harmonic state, where they interact with the 7-axis resonance but remain invisible to our current detectors. These sterile neutrinos would still participate in neutrino oscillations, but their oscillatory path would exist in a higher-dimensional space.
Sterile Neutrino Harmonic Formula:
P(\nu_{\alpha} \rightarrow \nu_s) = 7 \times \sin^2(2\theta_s) \times \sin^2\left(\frac{\Delta m_s^2 L}{4 E}\right)
Where:
P(\nu_{\alpha} \rightarrow \nu_s) is the probability of a neutrino changing from a known flavor to a sterile neutrino.
\theta_s is the oscillation angle between active and sterile neutrinos.
\Delta m_s^2 is the mass difference between active and sterile neutrinos.
This formula offers a pathway to designing neutrino oscillation experiments aimed at detecting the presence of sterile neutrinos. By tuning detectors to the 7-axis harmonic frequencies, we could capture evidence of sterile neutrinos oscillating between visible flavors and higher-dimensional states.
Step 4: Experimental Applications in Neutrino Physics
To test the harmonic resonance model of neutrinos proposed by Unified Fields Theory 1, several key experiments could be designed:
1.Long-Baseline Neutrino Oscillation Experiments:
Modify current neutrino oscillation experiments (like DUNE or T2K) to include harmonic resonance detectors that capture the oscillatory patterns predicted by the 7-axis model. These experiments would look for specific resonance frequencies as neutrinos oscillate between flavors.
2.Sterile Neutrino Search Using Harmonic Detectors:
Design a sterile neutrino detector that captures the resonance patterns of higher-dimensional oscillations. This could involve building detectors sensitive to harmonic transitions in neutrino oscillation experiments, allowing scientists to capture interactions that don’t occur within the standard three-dimensional framework.
3..Harmonic Neutrino Mass Measurement:
Develop new mass measurement techniques based on harmonic resonance. These would focus on measuring the energy and mass differences between neutrino flavors in a way that ties directly to their quantized harmonic states. This could improve the accuracy of neutrino mass hierarchies and offer insights into their role in dark matter.
Step 5: Potential Discoveries and Impact
The harmonic framework of Unified Fields Theory 1 has the potential to revolutionize our understanding of neutrinos and their role in the universe. Here are some groundbreaking discoveries that could result from these experiments:
1.Discovery of New Neutrino Flavors:
By applying harmonic resonance principles, scientists could discover new neutrino flavors beyond the standard three, including sterile neutrinos that interact with the universe through higher-dimensional fields.
2.Precision Mass Measurement:
Using harmonic oscillation data, we could refine our measurements of neutrino masses and solve the mass hierarchy problem, leading to more accurate predictions of neutrino behavior in both particle physics and cosmology.
3.Link to Dark Matter:
The discovery of sterile neutrinos or other higher-dimensional neutrino states could provide the missing link between neutrino physics and dark matter, helping to explain one of the most persistent mysteries in the universe.
Conclusion: Unified Fields Theory 1 and Neutrino Physics
By applying Unified Fields Theory 1 to the study of neutrino oscillations, mass hierarchies, and the potential discovery of sterile neutrinos, we open new doors to understanding one of the universe’s most enigmatic particles. The 7-axis harmonic resonance model provides a powerful framework for exploring how neutrinos oscillate between flavors, gain mass, and interact with dark matter and other unseen forces. With the right experimental designs, this theory could lead to groundbreaking discoveries in particle physics and help answer some of the most fundamental questions about the nature of matter and energy.

“For God so loved the world, that He gave His one and only Son, so that whoever believes in Him shall not perish, but have eternal life”
John 3:16 - 17
…for God did not send His Son into the world to condemn the world, but to save the world through Him.”
“For this is contained in Scripture:
“Behold, I am laying in Zion a choice stone, a precious cornerstone,
And the one who believes in Him will not be put to shame.”
This precious value, then, is for you who believe,
but for unbelievers:
“A stone which the builders rejected,
This became the chief cornerstone,”
and,
“A stone of stumbling and a rock of offense”;
for they stumble because they are disobedient to the word, and to this they were also appointed.
But you are a chosen people, a royal priesthood, a holy nation, a people for God’s own possession, so that you may proclaim the excellencies of Him who has called you out of darkness into His marvelous light.”
1 Peter 2:6-9

“For it is written; I will destroy the wisdom of the wise,
And the understanding of those who have understanding, I will confound.
Where is the wise person?
Where is the scribe?
Where is the debater of this age?
Has God not made foolish the wisdom of the world?
For since in the wisdom of God
the world through its wisdom did not come to know God,
God was pleased through the foolishness of the message preached to save those who believe.
For indeed Jews ask for signs and Greeks search for wisdom;
but we preach Christ crucified, to Jews a stumbling block, and to Gentiles foolishness,
but to those who are the called, both Jews and Greeks,
Christ the power of God and the wisdom of God.
For the foolishness of God is wiser than mankind,
and the weakness of God is stronger than mankind.”
1 Corinthians 1:19-25
In the beginning was 1. The Big Bang of math. 1 begot 2 and the 2’s had a 3 in 1-2 harmony. Alphabet too… easy as 1 2 3 in 4 parts back in 321 for a perfect 7 harmony. Short story by Phil Seawolf to provide some insight.
Jesus is the Chief Cornerstone 7 (Alpha to Omega)