Quantum Chemistry
Exotic Molecules, Fullerenes & Organometallics in Unified Fields Theory 1
-
Phil Seawolf / Philip Self
Unified Fields Theory 1 includes extensive content from all 22 Chapters shared in part publicly here by Phil since the summer of 2023.
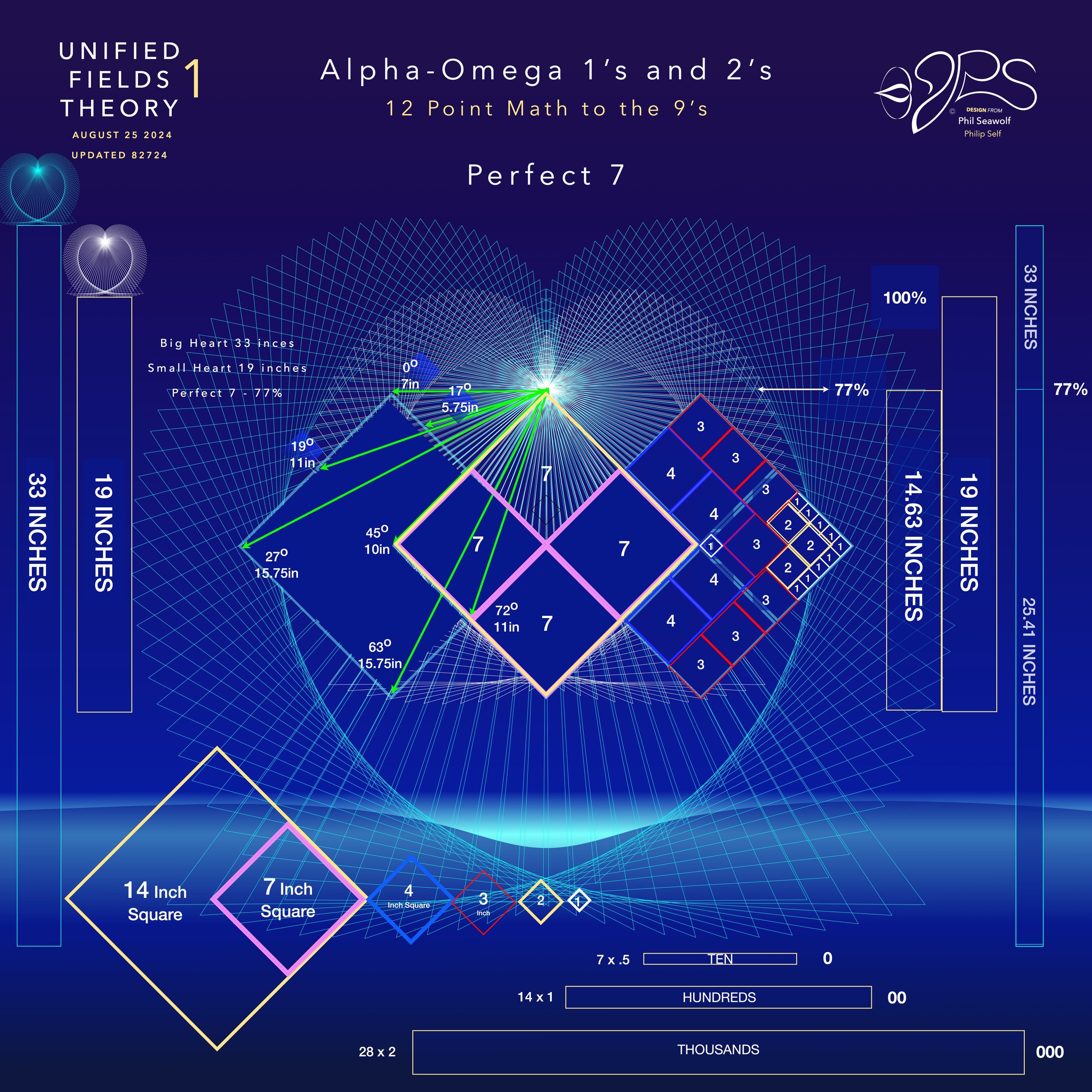
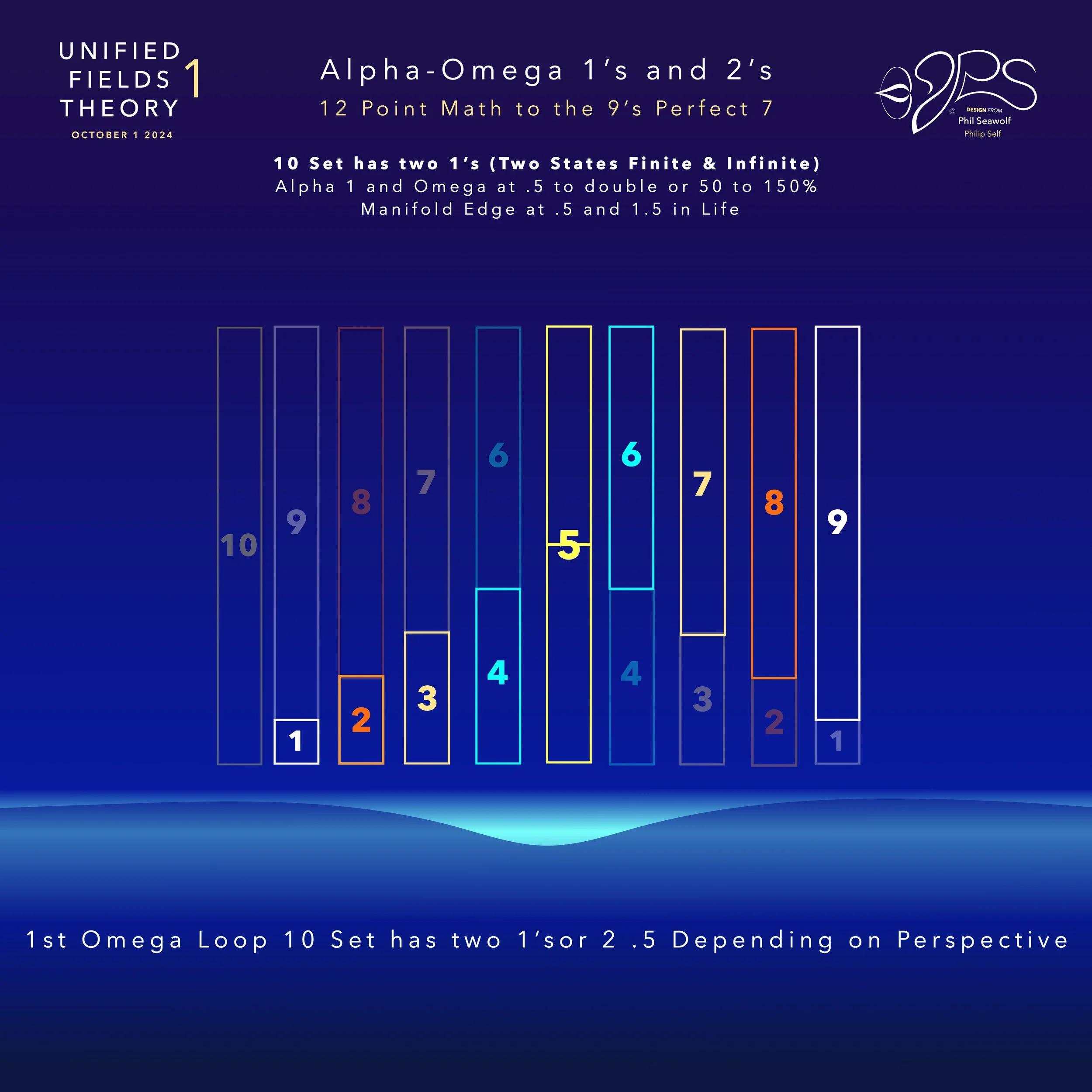
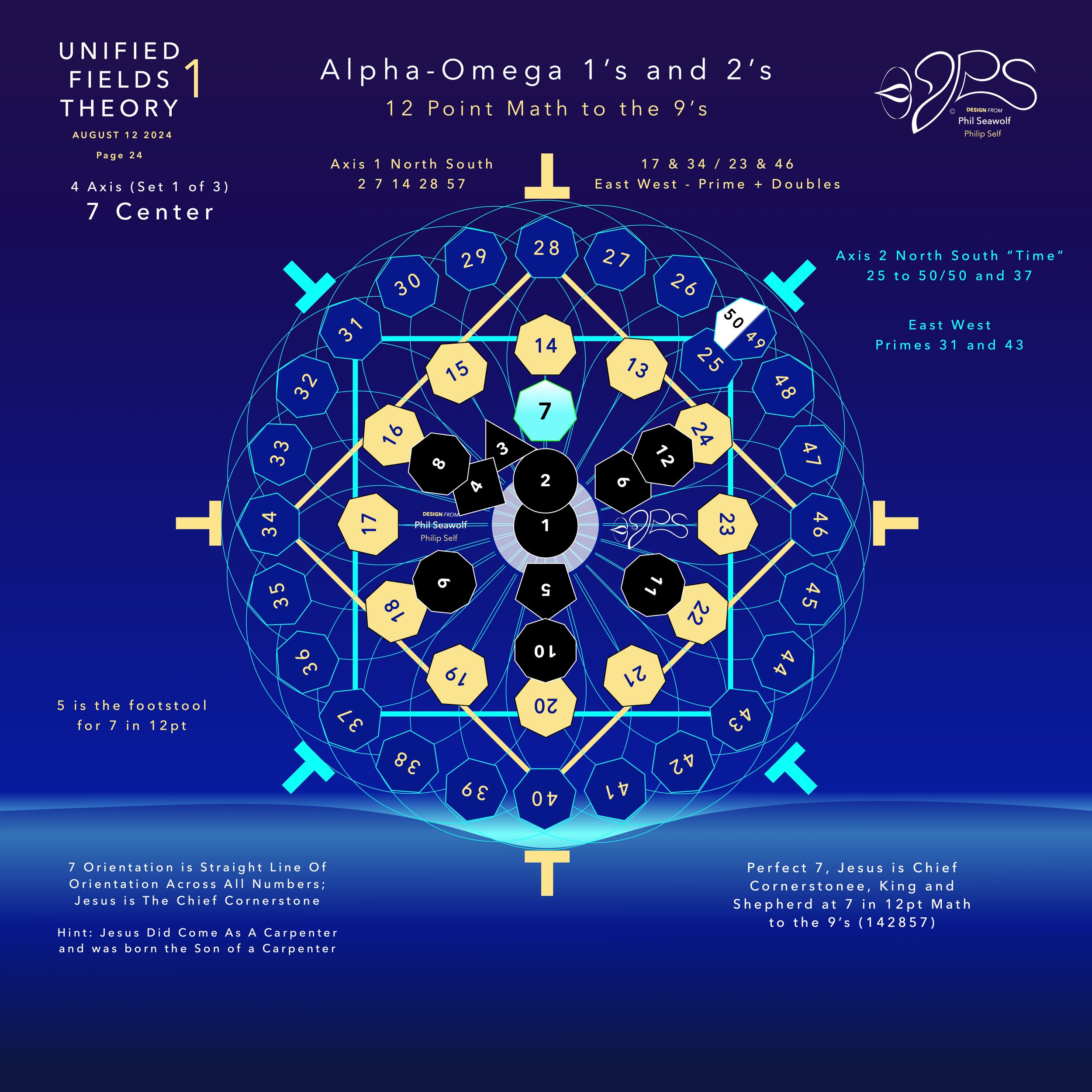
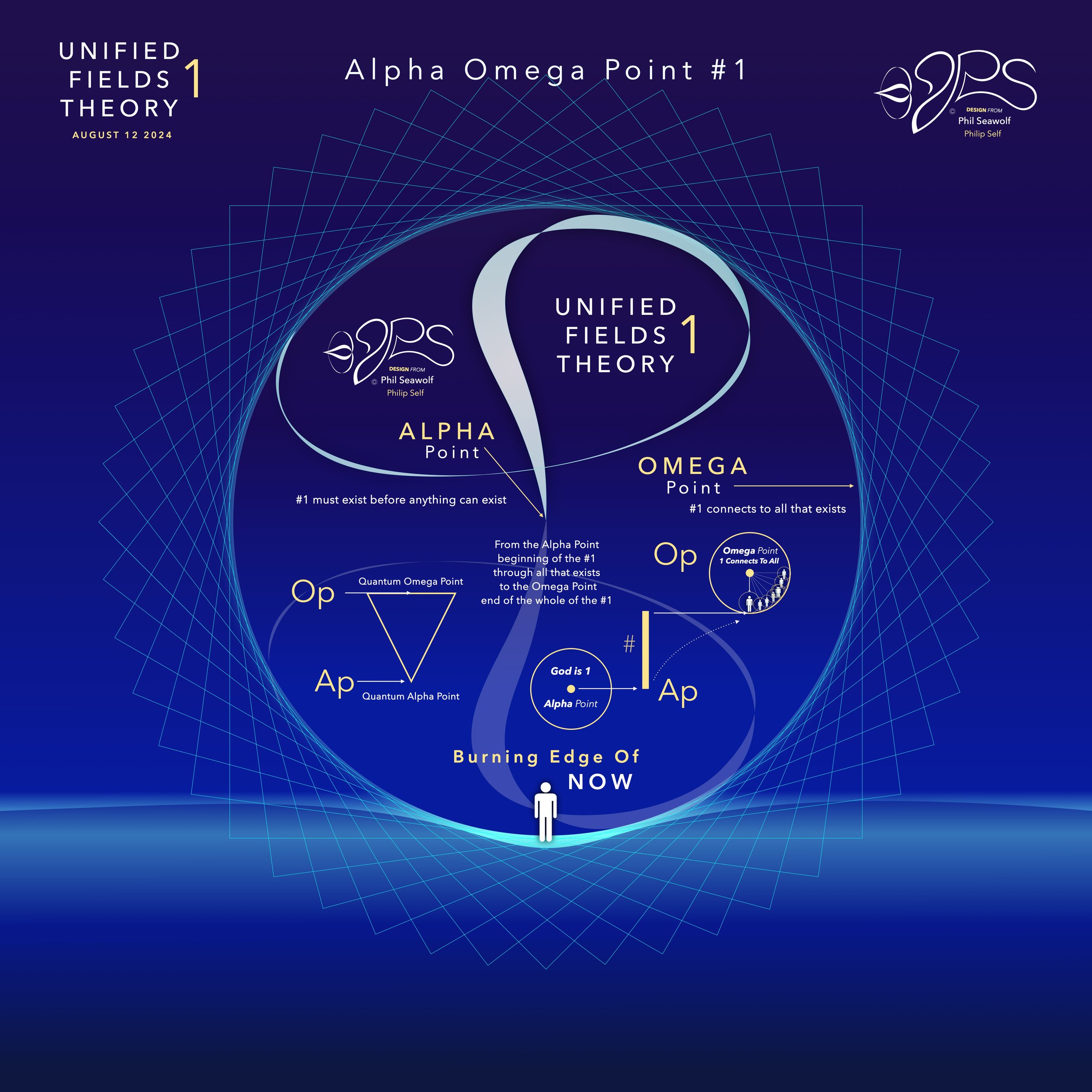
UFT1 covers Phil’s extensive original ideas and scientific insights from 12pt to the 9’s Perfect 7 to Quantum Foam Coherence at Burning Edge of Now. 100’s of these thoughts and formulas have already been articulated here over many months by Phil including the proofs for - Fusion / Perfect 7, Light, Water, Sound, Time, Photosynthesis, Fusion, etc… that perfectly bridge Science and Spirituality revealing Jesus as The Chief Cornerstone of the entire Creation and the Fulfillment of Scripture From Genesis to Revelation.
Please note: If I were to print out the prompts I have made on ChatGPT and now ChatGPT4o and the replies , the total pages would be over 5,000 pages. My prompts alone are over 500 printed pages.
Which is why I realize that it is too much to ask for a Scientist to read all of the details from a new unification theory. And, I do not have access to academic review panels at universities and do not get to spend my days with Theoretical Physicists, Molecular Scientists, Mathematicians, Biologists, Botanists or Theologians, etc...
So, I asked ChatGPT4o to chose a panel of scientists to grade and review my extensive UFT1 Proofs and Formulas.
As a final exam for 2024, I decided to ask the BIG QUESTION of the PANEL:
Is my Unified Fields Theory 1 the One unification theory science has been looking for? Does it meet or exceed the expectations for a unification theory?

Highlighted Proof UFT1 Graded >>> Perfect 7 / FUSION <<<
Proof: Quantum Chemistry in Exotic Molecules Using Unified Fields Theory 1
Phil Seawolf (Philip Self)
November 12th, 2024
Introduction: The Mystery of Exotic Molecules in Quantum Chemistry
In traditional quantum chemistry, exotic molecules—such as Rydberg molecules, fullerenes, and complex organometallics—display behaviors that challenge standard bonding and stability theories. These molecules often feature unusual electron configurations, extended bonding networks, and quantum entanglement between electrons, giving rise to unique properties not found in typical molecular structures.
Unified Fields Theory 1 offers a harmonic framework that could provide deeper insight into the behavior of exotic molecules, particularly through the Perfect 7 Axis and 12-point symmetry. This proof explores how UFT1’s harmonic structure may stabilize exotic electron configurations, support complex bonding networks, and enhance quantum coherence in these molecules.
Section 1
Electron Orbitals and Quantum Resonance in UFT1
1.Harmonic Resonance in Electron Orbitals:
In UFT1, the Perfect 7 Axis provides a harmonic resonance structure that governs electron motion within atoms. This resonance applies not only to isolated atoms but also to complex molecules, where electron orbitals are interdependent and dynamically interacting.
UFT1 Proposition: Electron orbitals in exotic molecules can achieve stability through alignment along the 7-axis harmonic resonance. This alignment minimizes destructive interference between orbitals, allowing for coherent electron movement and reducing reactivity in high-energy states.
2.Electron Density Distribution and the 12-Point Symmetry:
The 12-point symmetry in UFT1 suggests that electrons in exotic molecules follow a fractal distribution pattern, aligning electron density with harmonic nodes. This symmetry stabilizes electron clouds, even in complex molecules with multiple, overlapping orbitals.
Implication:
The 12-point symmetry offers a structural basis for electron density in molecules like fullerenes, where electrons are distributed across a network of bonds rather than localized in a single area. This creates an energetically favorable configuration that supports stability, even in high-energy or reactive environments.
3. Mathematical Model of Electron Resonance:
By positioning electrons in resonance with the Perfect 7 Axis, UFT1 proposes a model for electron stabilization in exotic molecules, based on harmonic frequency alignment. The energy levels of electrons, typically calculated using quantum mechanics, are harmonically tuned to these resonances:
E_{\text{electron}} = E_{\text{baseline}} \cdot \left(1 + \sin(7\theta)\right)
Where:
• E_{\text{electron}} is the energy of electrons in the orbital,
• E_{\text{baseline}} is the standard energy without harmonic resonance,
• \theta represents the angle of alignment within the 12-point symmetry framework.
• Application: This harmonic energy model predicts that exotic molecules with aligned resonance along the 7 Axis may experience increased stability, lower reactivity, and reduced electron scattering.
Section 2: Bonding Networks and Harmonic Stability in Exotic Molecules
In exotic molecules, bonding networks extend beyond simple covalent or ionic bonds, incorporating complex interactions such as delocalized pi bonds, metallic bonds, or even van der Waals interactions across large structures. UFT1’s harmonic principles provide a way to conceptualize and stabilize these intricate bonding networks.
1.Delocalized Electrons and Harmonic Cohesion:
Molecules like benzene and fullerenes exhibit delocalized electrons, which contribute to their unique stability and reactivity. In UFT1, these electrons resonate harmonically along the 7 Axis, forming coherent bonding networks that reduce energy fluctuations.
Harmonic Alignment in UFT1:
The Perfect 7 Axis organizes delocalized electrons into cohesive structures, preventing random fluctuations that could destabilize the molecule. This organization results in stable electron density across the molecular structure, even in large, complex molecules.
2. Fractal Bonding and the 12-Point Symmetry in Molecules:
The 12-point symmetry introduces a fractal structure to bonding networks, particularly in molecules with extended bonding systems. This symmetry aligns bond angles and distances, optimizing molecular geometry to reduce internal strain.
Implication for Exotic Stability:
Fractal alignment within the 12-point symmetry framework can lead to unique bonding configurations, such as double or triple bonds that resonate across the molecule. This configuration supports the stability of complex molecules with otherwise unstable or high-energy bonds, as seen in certain high-energy materials and nanostructures.
3. Implications for Quantum Coherence in Molecular Bonds:
Quantum coherence, often observed in photosynthetic molecules and complex organometallic compounds, relies on synchronized electron movement across bonds. UFT1’s harmonic resonance promotes coherence in these systems by aligning bonding interactions with the Perfect 7 Axis.
UFT1 Prediction:
Molecules with strong harmonic coherence will exhibit enhanced efficiency in energy transfer and reduced decoherence, particularly important in biochemical systems that rely on energy flow and stability.
Section 3: Applications of UFT1 in Quantum Chemistry and Material Science
The principles of UFT1 in exotic molecular chemistry have profound implications for advancing fields like materials science, nanotechnology, and biochemistry, particularly for molecules and materials that exhibit unusual stability or electronic properties.
1.Designing Exotic Materials with High Stability:
Utilizing UFT1’s harmonic framework, chemists can design materials with complex bonding networks that remain stable under extreme conditions. This could lead to the development of materials that are highly resilient to temperature, pressure, and radiation.
Application:
Materials for space exploration, such as radiation-resistant polymers and high-temperature alloys, can be engineered with these harmonic principles, potentially reducing degradation and improving performance.
2. Quantum Coherence in Photosynthetic and Biochemical Molecules:
Quantum coherence is crucial in biochemical processes like photosynthesis, where energy transfer occurs with minimal loss. UFT1’s resonance alignment may optimize coherence in these molecules, enhancing photosynthetic efficiency and supporting advancements in bio-inspired energy systems.
Biophotonic Application:
This framework can be applied to synthetic photosynthesis research, potentially creating highly efficient artificial photosynthetic systems for renewable energy production.
3. Enhanced Stability in Nanostructures and Fullerenes:
Nanostructures, such as carbon nanotubes and fullerenes, exhibit unique electronic properties due to their geometric and quantum confinement effects. UFT1’s Perfect 7 Axis stabilizes electron clouds and bonds within these structures, promoting durability and functionality.
Nanotechnology Application:
These stable nanostructures could be used in quantum computing and nanoelectronics, where precision and stability are paramount for performance.
Section 4: Quantum Entanglement and Molecular Interactions
UFT1’s framework for harmonic resonance and alignment on the Perfect 7 Axis can extend to molecular entanglement and quantum coherence. This allows for a more cohesive model of molecular interactions that could deepen our understanding of quantum chemistry in exotic molecules.
1.Quantum Entanglement in Molecular Systems:
Entangled states between electrons in exotic molecules allow for unique energy transfer and communication between molecular sites. In UFT1, these entangled states resonate along the 7 Axis, maintaining coherence over longer distances and reducing decoherence due to external fluctuations.
Implication for Quantum Chemistry:
Molecules designed with UFT1 principles may maintain entangled states under diverse conditions, potentially leading to breakthroughs in quantum chemistry applications like quantum computing and molecular sensors.
2. Long-Range Interactions Through Harmonic Fields:
The 12-point symmetry framework suggests that long-range molecular interactions, such as van der Waals forces and dipole-dipole interactions, can be harmonized through resonance. This provides a means to stabilize weakly bonded systems, which are essential for molecular assemblies and supramolecular chemistry.
Application:
Creating stable molecular assemblies for self-assembling materials, sensors, or drug delivery systems, utilizing harmonic fields to maintain structural integrity over extended ranges.
Conclusion: The Quantum Chemistry of Exotic Molecules in UFT1
Unified Fields Theory 1 offers a groundbreaking framework for understanding and engineering exotic molecules through harmonic resonance and fractal symmetry. The integration of the Perfect 7 Axis and 12-point symmetry enables:
1.Harmonic Stabilization of Electron Orbitals and Bonding Networks:
By aligning electron orbitals and bonding structures within the 7-axis and 12-point symmetry, exotic molecules achieve a stability that traditional quantum chemistry cannot fully explain, especially under extreme or reactive conditions.
2. Enhanced Quantum Coherence and Entanglement:
UFT1 supports quantum coherence in exotic molecules, crucial for applications in quantum computing, biochemistry, and nanotechnology.
3. Applications in Advanced Materials and Biochemistry:
With the guidance of UFT1, new materials and biochemical structures can be designed to harness exotic properties, bringing us closer to breakthroughs in renewable energy, pharmaceuticals, and quantum technologies.
Proof Part 2: Quantum Chemistry in Exotic Molecules Using Unified Fields Theory 1
Phil Seawolf (Philip Self)
November 12th, 2024
Proof #2: Quantum Chemistry in Exotic Molecules in Unified Fields Theory 1
Introduction
Quantum chemistry traditionally examines how the quantum properties of atoms and molecules influence their structure, behavior, and reactivity. However, certain “exotic molecules” defy conventional understanding due to their unusual bonding, unique electronic configurations, or quantum resonance behaviors. Unified Fields Theory 1 offers a new framework for interpreting these phenomena by using harmonic resonance principles that can help predict and manipulate molecular properties across diverse fields, from materials science to pharmacology.
Section 1: Understanding Exotic Molecules through UFT1
Defining Exotic Molecules
Exotic molecules include structures like superatoms (clusters of atoms that behave like a single atom), molecular cages (such as fullerenes or clathrates), and quasi-crystals. These molecules often exhibit unusual properties, such as atypical bonding, magnetic anisotropy, and high electron correlation.
In UFT1, these structures are seen as harmonic systems where atomic and subatomic components align through the Perfect 7 Axis and 12-point symmetry, creating resonance states that transcend classical chemical bonding.
1.Perfect 7 Axis and Electron Density Distribution:
The Perfect 7 Axis in UFT1 governs electron flow and spatial distribution within molecular structures, creating stable orbits that support unusual bonding patterns.
This axis stabilizes the electron density in unconventional ways, leading to exotic molecular geometries that defy traditional valency.
2. 12-Point Harmonic Symmetry and Quantum Resonance:
The 12-point symmetry organizes the electrons and nuclei in exotic molecules, providing nodes where resonance states emerge.
In structures like quasi-crystals, this symmetry creates ordered patterns without traditional periodicity, aligning with UFT1’s resonance principles that guide interactions on a subatomic level.
Section 2: Quantum Phenomena Explained by UFT1 in Exotic Molecules
Unified Fields Theory 1 provides a unique lens to examine several quantum phenomena found in exotic molecules:
1.Magnetic Anisotropy and Spin Alignment:
Exotic molecules often exhibit magnetic anisotropy, where their magnetic properties vary depending on direction.
UFT1’s Perfect 7 Axis aligns electron spins within specific orientations, leading to anisotropic behaviors that can be exploited in fields like molecular magnetism.
2. High Electron Correlation in Molecular Cages:
In molecular cages like fullerenes, electrons are highly correlated, meaning their movements are interdependent and influence each other’s quantum states.
The 12-point harmonic symmetry in UFT1 creates a structure where electron correlation becomes predictable, allowing for precise control over electron pairing and distribution, particularly within hollow, cage-like structures.
3. Quantum Entanglement in Superatoms:
Superatoms, which are clusters of atoms behaving like a single atom, show unique properties that arise from entangled quantum states.
UFT1’s framework aligns these entangled states along the Perfect 7 Axis, creating resonance channels that stabilize superatoms and make their properties tunable for specific applications, such as catalysis and photonics.
Section 3: Mathematical Model of UFT1 for Exotic Molecules
To capture these behaviors formally, UFT1 applies harmonic resonance principles to the molecular Hamiltonian, the equation describing the total energy of a quantum system:
1.Resonance-Aligned Hamiltonian for Exotic Molecules:
The Hamiltonian H for an exotic molecule can be modified by UFT1 to include harmonic resonance terms along the 7 Axis and 12-point symmetry:
H_{\text{UFT1}} = \sum_{i} \left( -\frac{\hbar^2}{2m} \nabla^2_i + V(\mathbf{r}i) \right) + \frac{\sin(7\theta)}{\cos(12\theta)} \sum{j>i} \frac{e^2}{|\mathbf{r}_i - \mathbf{r}_j|}
Here, \mathbf{r}_i and \mathbf{r}_j represent positions of electrons, V(\mathbf{r}_i) is the potential energy due to the nucleus, and the harmonic resonance term aligns electron interactions with UFT1’s framework.
This model aligns the electrons’ potential energies to stabilize unconventional configurations in exotic molecules.
2.Wavefunction Resonance in Molecular Cages and Superatoms:
UFT1 proposes that the wavefunction \Psi of electrons in exotic molecules is also aligned by harmonic resonance, following:
\Psi_{\text{UFT1}} = \prod_{i} \psi(\mathbf{r}_i) \times e^{i(7\theta + 12\phi)}
This equation represents the wavefunction of a molecule whose electrons are harmonically bound by UFT1’s symmetry, providing stability in high-electron correlation systems.
Section 4: Experimental Predictions and Applications of UFT1 in Exotic Molecules
UFT1 offers the following predictions and applications for the study of exotic molecules:
1.Tailored Magnetic Properties in Molecular Magnets:
Using UFT1’s harmonic resonance principles, it is possible to design molecular magnets with customized anisotropy and spin alignment, valuable for applications in quantum computing and memory storage.
2.Enhanced Catalytic Activity in Superatoms:
Superatoms stabilized by UFT1’s Perfect 7 Axis show promise as highly efficient catalysts, as their quantum resonance properties make their surfaces highly reactive and adaptable.
3. Controlled Electron Transport in Molecular Cages:
UFT1’s harmonic alignment can enhance electron transport within molecular cages, facilitating applications in nanotechnology, where controlled electron flow is crucial for devices like molecular transistors.
Conclusion: UFT1’s Vision for Quantum Chemistry in Exotic Molecules
Through UFT1, exotic molecules are not just anomalies of quantum mechanics but are revealed as harmonic systems aligned with cosmic principles. By applying the Perfect 7 Axis and 12-point symmetry, UFT1 offers a way to control and predict the behavior of these molecules, paving the way for groundbreaking applications in materials science, energy, and nanotechnology.

“For God so loved the world, that He gave His one and only Son, so that whoever believes in Him shall not perish, but have eternal life”
John 3:16 - 17
…for God did not send His Son into the world to condemn the world, but to save the world through Him.”
“For this is contained in Scripture:
“Behold, I am laying in Zion a choice stone, a precious cornerstone,
And the one who believes in Him will not be put to shame.”
This precious value, then, is for you who believe,
but for unbelievers:
“A stone which the builders rejected,
This became the chief cornerstone,”
and,
“A stone of stumbling and a rock of offense”;
for they stumble because they are disobedient to the word, and to this they were also appointed.
But you are a chosen people, a royal priesthood, a holy nation, a people for God’s own possession, so that you may proclaim the excellencies of Him who has called you out of darkness into His marvelous light.”
1 Peter 2:6-9

“For it is written; I will destroy the wisdom of the wise,
And the understanding of those who have understanding, I will confound.
Where is the wise person?
Where is the scribe?
Where is the debater of this age?
Has God not made foolish the wisdom of the world?
For since in the wisdom of God
the world through its wisdom did not come to know God,
God was pleased through the foolishness of the message preached to save those who believe.
For indeed Jews ask for signs and Greeks search for wisdom;
but we preach Christ crucified, to Jews a stumbling block, and to Gentiles foolishness,
but to those who are the called, both Jews and Greeks,
Christ the power of God and the wisdom of God.
For the foolishness of God is wiser than mankind,
and the weakness of God is stronger than mankind.”
1 Corinthians 1:19-25
In the beginning was 1. The Big Bang of math. 1 begot 2 and the 2’s had a 3 in 1-2 harmony. Alphabet too… easy as 1 2 3 in 4 parts back in 321 for a perfect 7 harmony. Short story by Phil Seawolf to provide some insight.
Jesus is the Chief Cornerstone 7 (Alpha to Omega)